
Здравствуйте, уважаемые читатели! На днях приходил клиент, которому срочно нужны были деньги для ремонта автомобиля.
Хотел оформить кредит, предварительно был ознакомлен со всеми условиями и графиком платежей. Но тут он пришел и сказал, что мы неправильно считаем сумму платежа.
Только через минут 15 выяснилось, что он не увидел схему погашения кредита, а она там была указана аннуитетной. Пришлось ему еще подробно объяснять, как рассчитать аннуитетный платеж по кредиту. Сейчас хочу поделиться и с вами этой несложной формулой расчета.
Содержание статьи:
- Аннуитетные платежи — расчёт, формула
- Расчет аннуитетного платежа по кредиту — калькулятор, формулы
- Расчет аннуитетных платежей: формула, использование Excel
- Кредитный калькулятор. Формулы аннуитетного и дифференцированного платежа. Что выгоднее?
- Расчет аннуитетного платежа
- Расчет аннуитетных платежей по кредиту в Excel
- Кому выгоден аннуитет?
Аннуитетные платежи — расчёт, формула
Аннуитетный платеж — вариант ежемесячного платежа по кредиту, когда размер ежемесячного платежа остаётся постоянным на всём периоде кредитования.
Ежемесячный платёж, при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа идёт на погашение процентов за пользование кредитом. Вторая часть идёт на погашение долга.
При аннуитетной схеме выплат по кредиту, ежемесячный платёж рассчитывается как сумма процентов, начисленных на текущий период и суммы идущей на погашения суммы кредита.
Для расчёта размера ежемесячного платежа можно воспользоваться кредитным калькулятором. С помощью калькулятора кредитов можно определить размер начисленных процентов, а так же сумму, идущую на погашение долга. Кроме того, можно взять в руки обычный калькулятор и рассчитать график платежей вручную.
Расчёт
Рассчитать месячный аннуитетный платеж можно по следующей формуле:

где: x – месячный платёж, S – первоначальная сумма кредита, P – (1/12) процентной ставки, N – количество месяцев.
Формула, для определение того, какая часть платежа пошла на погашение кредита, а какая на оплату процентов является достаточно сложной и без специальных математических знаний простому обывателю будет сложно ей воспользоваться. Поэтому мы рассчитаем данные величины простым способом, дающим такой же результат.
Для расчета процентной составляющей аннуитетного платежа, нужно остаток кредита на указанный период умножить на годовую процентную ставку и всё это поделить на 12 (количество месяцев в году).

Что бы определить часть, идущую на погашение долга, необходимо из месячного платежа вычесть начисленные проценты.

Поскольку часть, идущая на погашение основного долга зависит от предыдущих платежей, поэтому рассчёт графика, по данной методике вычислять последовательно, начиная с первого платежа.
Пример расчёта графика выплат по аннуитетному кредиту
Для примера рассчитаем график платежей по кредиту в размере 100000 р. и годовой процентной ставкой 10%. Сроком погашения кредита возьмём 6 месяцев.
Для начала рассчитаем ежемесячный платёж.

Затем рассчитаем по месяцам процентную и кредитную часть аннуитетного платежа.
- 1 месяц
- Проценты: 100000 * 0,1 / 12 = 833,33
- Основной долг: 17156,14 – 833, 33 = 16322,81
- 2 месяц
- Остаток кредита: 100000 – 16322,81 = 83677,19
- Проценты: 83677,19 * 0,1/12 = 697,31
- Основной долг: 17156,14 – 697,31 = 16458,83
- 3 месяц
- Остаток кредита: 83677,19 — 16458,83 = 67218,36
- Проценты: 67218,36 *0,1/12 = 560,15
- Основной долг: 17156,14 – 560,15 = 16595,99
- 4 месяц
- Остаток кредита: 67218,36 — 16595,99 = 50622,38
- Проценты: 50622.38 * 0,1/12 = 421.85
- Основной долг: 17156,14 – 421,85 = 16734,29
- 5 месяц
- Остаток кредита: 50622,38 — 16734,29 = 33888,09
- Проценты: 33888,09 * 0,1/12 = 282,40
- Основной долг: 17156,14 – 282,40 = 16873,74
- 6 месяц
- Остаток кредита: 33888.09 — 16873.74 = 17014,35
- Проценты: 17014,35 * 0,1/12 = 141,79
- Основной долг: 17156,14 – 141,79 = 17014,35
Если интересно узнать размер переплаты по аннуитетному кредиту, необходимо ежемесячный платёж, умножить на количество периодов и из получившегося числа вычесть первоначальный размер кредита. В нашем случае переплата будет следующей:
17156,14 * 6 – 100000 = 2936,84
источник: http://kredityvopros.ru/www.platesh.ru/annuitetnie-plateshi/
Расчет аннуитетного платежа по кредиту — калькулятор, формулы
Аннуитетный платеж – это наиболее распространенный вариант ежемесячного платежа по кредиту. В этом случае его размер остается неизменным.
Из чего складывается?
Как уже было сказано, при аннуитетной схеме погашения задолженности по кредиту размер ежемесячного платежа остается постоянным в течение всего периода кредитования.
При этом платеж состоит из 2-х частей: первая из которых идет на погашение процентов за пользование кредитом, а вторая – на погашение долга.
Ежемесячный платеж складывается из суммы процентов, которые начисляются на текущий период, и суммы, идущей на погашение «тела» кредита.
Расчет размера ежемесячного аннуитетного платежа можно произвести с помощью кредитного калькулятора. Воспользовавшись им, можно определить как размер начисляемых процентов, так и сумму, которая идет на погашение долга. Но, чтобы лучше разобраться в том, откуда берутся суммы выплат, можно произвести расчеты вручную, с помощью обычного калькулятора.
Расчет аннуитетного платежа по формуле
Для расчета месячного аннуитетного платежа по кредиту надо воспользоваться следующей формулой:

Приведем условный пример расчета аннуитетного платежа, взяв за основу следующие условия:
- S (сумма кредита) – 20 000 рублей;
- P (годовая процентная ставка по кредиту) – 22% «годовых»;
- m – месячная процентная ставка (она вычисляется по следующей формуле: P/100/12).
- В нашем случае месячная процентная ставка составляет: 22:100:12= 0,0183.
- N – срок кредитования – 24 месяца (количество процентных периодов).

Это означает, что на протяжении двух лет вам придется вносить в банк каждый месяц по 1037 руб. 20 коп.
Чтобы посчитать размер переплаты, достаточно будет умножить размер ежемесячного платежа на количество месяцев (1 037.20×24=24 892.80) и от полученного числа отнять сумму кредита (24 892.80-20 000 = 4 892.80).
Из этого следует, что размер переплаты по описываемому аннуитетному кредиту составляет 4 892 руб. 80 коп.
Тот же результат мы получим, если введем данные в калькулятор кредитного платежа (имеющиеся небольшие расхождения наших расчетов с приведенными в таблице можно объяснить разным округлением малых долей, а в случае с калькуляторами конкретных банков, – и с возможными дополнительными процентами).
Таблица расчета ежемесячных аннуитетных платежей, расчета ежемесячных процентов по кредиту и размера погашения части кредита имеет следующий вид:

Расчет аннуитетного платежа — калькурятор в программе Excel
Можно сделать расчет аннуитетного платежа и в Excel, для чего здесь имеется специальная функция – ПЛТ. Нажав на значок «fx» который находится слева от поисковика, вы получите список функций в новом окне. Среди них будет и ПЛТ. Выберите ее и нажмите «ОК».
Перед вами появится другое окно, где Вам нужно будет заполнить следующие строки: «Ставка» — 22%/12; «Кпер» -24; «Пс» — -20000 (не забудьте, что число ставится с минусом!). Под строками сразу же появится число 1 037,56 – сумма, которую нужно будет вносить ежемесячно. Когда нажмете «ОК», то это же число появится в ячейке таблицы.
Как видите, вычислить размер аннуитетного платежа самостоятельно – совсем несложно. Но, отправляясь в банк, чтобы оформить кредит, нужно все-таки быть готовым к тому, что ежемесячный взнос будет несколько больше – за счет дополнительных комиссий.
источник: http://kredityvopros.ru/101.credit/articles/kredity/annuity/
Расчет аннуитетных платежей: формула, использование Excel
Если вы берете кредит, то обязуетесь погашать ссуженную сумму и проценты за пользование ею на протяжении определенного срока. Для того чтобы клиенту было ясно, как и в какие сроки следует вносить проплаты, составляют графики погашения.
Наиболее распространенный вариант – внесение аннуитетных платежей, то есть выплата кредита равными суммами.
Как рассчитать размер аннуитетного платежа?
Существует специальная формула, которая позволяет рассчитать сумму, которую ежемесячно следует вносить для погашения долга перед банком и процентов по нему.
А = К х S
В этой формуле: A – размер платежа, K – коэффициент аннуитета, S – сумма полученного кредита
Есть один неизвестный элемент формулы – коэффициент аннуитета. Его необходимо рассчитать отдельно по соответствующей формуле.

Здесь i – это месячная ставка процентов за пользование кредитом, которая рассчитывается путем деления годовой ставки на 12 месяцев, n – количество месяцев, на протяжении которого кредит необходимо погасить.
Эта формула поможет вам самостоятельно рассчитать сумму, которую следует вносить каждый месяц в пользу банка.
Как рассчитать аннуитетные платежи в Excel
Чтобы не утруждать себя расчетами вручную, попробуйте сделать это при помощи таблицы Excel. Там есть специальная функция под названием ПЛТ. Для расчетов следует создать новую таблицу и ввести строку в любой ячейке.
Если вам выдали кредит в сумме 30000 руб., под 18% годовых на 36 месяцев, необходимо ввести в ячейку вот такое выражение. = ПЛТ(18%/12; 36; -30000)
В скобках вы вводите данные в таком порядке: размер процентной ставки, количество месяцев внесения проплат, сумма, полученная в долг. Минус перед 30000 как раз и означает долговое обязательство, в принципе, ставить его необязательно, если только вы не используете форулу для более сложных вычислений и знак принципиально важен.
Можно внести запись и в таком виде: =ПЛТ(0,015; 36; -30000)
Получается 1084,57 рублей.
Если лень вбивать формулу — просто скачайте готовый файл с формулой аннуитета или же обратитесь к кредитному калькулятору.
Произведенные расчеты помогут вам удостовериться, что сотрудники банка верно исчислили суммы, на которую ежемесячно будет уменьшаться ваш бюджет.
Справка: аннуитетные и дифференцированные платежи
По аннуитетной схеме клиент ежемесячно вносит в счет погашения кредита и процентов по нему одинаковую сумму. Так происходит на протяжении всего срока действия договора с финансовым учреждением.
Банкам выгоднее предлагать клиентам схему с аннуитетными платежами, так как в таком случае они больше зарабатывают за счет большей суммы процентов. И клиентам удобнее такая схема, так как каждый месяц нужно вносить одинаковую сумму. Это не требует излишних затрат времени на уточнение того, какую сумму нужно вносить.
источник: http://kredityvopros.ru/biznes-kredit.info/malyj/raschet-annuitetnyh-platezhej-formula-excel.html
Кредитный калькулятор. Формулы аннуитетного и дифференцированного платежа. Что выгоднее?
Кредитный калькулятор использует стандартные формулы, и взяв обычный калькулятор вы сможете легко проверить полученный результат, по приведенным ниже формулам.
Кредитный калькулятор — помогает рассчитывать ежемесячную сумму выплат на погашение кредита, эффективную процентную ставку по формуле Центрального Банка РФ, так же вы сможете узнать, какая часть выплат идет на погашение основной кредитной суммы, а какая часть на погашение процентов по кредиту.
Калькулятор дает возможность расчета по двум видам платежей:
- аннуитетный платеж — это равный по сумме ежемесячный платеж по кредиту, который включает в себя сумму начисленных процентов за кредит и сумму основного долга, применяется в большинстве коммерческих банков;
- дифференцированный платеж — это ежемесячный платеж, уменьшающийся к концу срока кредитования, и состоит из выплачиваемой постоянной доли основного долга и процентов на невыплаченный остаток кредита, часто используется в СберБанке.
Калькулятор кредитный — применяется для сравнения различных типов займов и получения нужной информации не прибегая к помощи банковских специалистов.
Расчет дифференцированного платежа
Дифференцированные платежи в начале срока кредитования больше, а затем постепенно уменьшаются, т.е. регулярные платежи по кредиту не равны между собой.
Структура дифференцированного платежа состоит из двух частей: фиксированной на весь период суммы, идущей на погашение суммы задолженности, и убывающей части — процентов по кредиту, которая рассчитывается от суммы остатка заложенности по кредиту.
Для того чтобы вычислить сумму возврата основного долга, необходимо первоначальную сумму кредита разделить на срок кредита (количество периодов):

где ОД — возврат основного долга; СК — первоначальная сумма кредита; КП — количество периодов.
На этом сходство в подходах банков заканчивается, и начинаются различия. Состоят они в подходах к вычислению суммы причитающихся процентов. Основных подходов два, разница — в используемой временной базе. Часть банков исходят из того, что «в году 12 месяцев», и тогда размер ежемесячных процентных выплат определяется по формуле:

где НП — начисленные проценты; ОК — остаток кредита в данном месяце; ПС — годовая процентная ставка.
Часть банков исходит из того, что «в году 365 дней» и такой подход называется расчетом точных процентов с точным числом дней ссуды. Размер ежемесячных процентных выплат в данном случае определяется по формуле:

где НП — начисленные проценты; ОК — остаток кредита в данном месяце; ПС — годовая процентная ставка; ЧДМ — число дней в месяце (понятно, что это число меняется от 28 до 31).
Пример 1. В качестве примера приведен график платежей для кредита в размере 1 000 условных единиц на срок 12 месяцев, с ежемесячным возвратом 1/12 части кредита и уплатой процентов. В этом примере при расчете начисленных процентов используется формула № 2. («в году 12 месяцев»).

При расчете необходимо учитывать погрешности округления.
Расчет аннуитетного платежа
Аннуитетными, т.е. равновеликими платежами называют платежи, которые производятся на протяжении всего срока кредита равными друг другу. При таком виде платежа заемщик регулярно совершает платеж одного и того же размера. Эта сумма может меняться только по соглашению сторон или в некоторых случаях частичного досрочного погашения.
Структура аннуитетного платежа также состоит из двух частей: процентов за пользование кредитом и суммы идущей на погашение кредита. С течением времени соотношение этих величин меняется и проценты постепенно начинают составлять меньшую величину, соответственно сумма на погашение основного долга внутри аннуитетного платежа увеличивается.
Поскольку, при аннуитетных платежах в начале сумма, идущая на погашение основного долга, убывает медленно, а проценты всегда начисляются на остаток от этой суммы, то и общий размер уплаченных процентов по такому кредиту больше.
Это особенно заметно при досрочных погашениях. В первые периоды кредитования основные выплаты приходятся именно на погашение процентов по кредиту.
Величина аннуитетного платежа определяется по формуле:

где АП — аннуитетный платеж; ПС — процентная ставка за период начисления; СК — первоначальная сумма кредита; КП — количество периодов.
Т.е. если платежи ежемесячные, то КП – срок в месяцах, а ПС месячная процентная ставка (1/12 годовой)
Расчет аннуитетных платежей по этой формуле, можно производить с помощью MS Excel и встроенной функции рабочего листа PMT (в русских версиях ППЛАТ или ПЛТ)
Пример 2. В качестве примера приведен график аннуитетных платежей для кредита в размере 1 000 условных единиц на срок 12 месяцев.

При расчете необходимо учитывать погрешности округления.
Другие формулы для расчета аннуитетного платежа
Некоторые кредитные организации применяют формулу, где первый платеж — не аннуитетный:
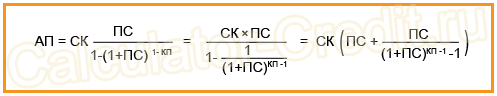
где АП — аннуитетный платеж; ПС — процентная ставка за период начисления; СК — первоначальная сумма кредита; КП — количество периодов.
Первый платеж предварительный — не аннуитетный. Он всегда, якобы, меньше АП, т.к. включает в себя только проценты за первый период, который может быть полным или неполным. Но при полном периоде — 31 день, при высоких ПС и долгосрочном кредитовании предварительный платеж может быть больше АП! Оставшиеся (КП–1) платежей – аннуитетные. Эта формула используется в АИЖК.
Также на практике встречается применение формулы, где первый и последний платежи – не аннуитетные:

где АП — аннуитетный платеж; ПС — процентная ставка за период начисления; СК — первоначальная сумма кредита; КП — количество периодов.
Первый и последний платежи не аннуитетные, первый — только проценты за первый период, а последний — остатки, “хвосты” и т.д.
Наименьший Аннуитетный Платеж получается при расчетах по формуле 4, наибольший — по формуле 6. Причем чем меньше АП остается до окончательного расчета, тем существеннее становится эта разница. Что особенно важно при досрочном погашении. Поэтому необходимо интересоваться не только процентной ставкой, но и формулой по которой рассчитываются АП.
Что выгоднее аннуитетная или дифференцированная схема платежей?
Вопросам выбора схемы платежа по ипотечному кредиту часто задаются потенциальные заемщики. Если сравнивать аннуитетную и дифференцированную схемы, то самыми очевидными различиями будут являться следующие:
- Неизменность размера регулярного платежа при аннуитетной схеме и постоянное убывание такого платежа при дифференцированной.
- Больший размер платежа, по сравнению с аннутетной схемой, в начале срока кредита при дифференцированной схеме.
- Аннуитетная схема выплат более доступна для заемщиков, т.к. выплаты равномерно распределяются на весь срок кредита. При выборе дифференцированных платежей подтвержденный доход заемщика или созаемщиков должен быть примерно на четверть больше, чем при аннуитетных платежах.
- При аннуитетных платежах в начале сумма основной задолженности убывает медленно, а и общий размер начисленных процентов больше. Если заемщик решит полностью погасить кредит досрочно, выплаченные вперед проценты будут потеряны. При аннуитетной схеме значительная часть процентов уплачивается с начала, обеспечивая выплаты на весь срок кредита. Поэтому при дифференцированных платежах досрочное погашение будет происходит без таких финансовых потерь даже в начале срока ипотечного кредита.
- Кредит с дифференцированным платежом труднее получить, т.к. при получении кредита оценивается платежеспособность заемщика. Дифференцированная схема в начале срока кредита предлагает значительно большие платежи, нежели аннуитетная. Это означает то, что заемщику необходимо иметь больший доход. В среднем считается, что доход заемщика при дифференцированной схеме должен быть больше на 20% выше, чем при аннуитетной схеме.
Подводя итог можно сказать, что вид платежа является одним из основных параметров кредита, однако рассматривать его необходимо в совокупности с другими параметрами.
источник: http://kredityvopros.ru/calculator-credit.ru/articles/credit-calc.html
Расчет аннуитетного платежа
Аннуитетные платежи – это такой вид платежей по кредиту, размер которых не меняется в течение всего срока действия договора. Каждый аннуитетный платеж состоит из двух частей – начисленных процентов и суммы, направляемой на погашение долга, соотношение этих частей постоянно меняется.
Расчет аннуитетного платежа осуществляется по формулам, выведенным математическим путем, но прежде чем вспоминать уроки математики, давайте разберемся в самом принципе расчета аннуитетного платежа. Для удобства обратимся к несложному примеру:
Вы взяли кредит на сумму 1 000 000,00 руб. под 12 % годовых на срок 200 месяцев при условии уплаты аннуитетных платежей в сумме 12 000 руб. каждый месяц.
Cумма аннуитета в нашем примере — произвольная, можно взять и другую, пока нам нужно просто понять сам принцип расчета.
Давайте вместе посчитаем, какую сумму процентов Вы должны заплатить банку за первый месяц пользования таким кредитом. Арифметика при расчете процентов очень простая:
1 000 000 рублей (сумма кредита) × 1 % (мы 12 % годовых делим на 12 месяцев в году) = 10 000 рублей.
Получается, совершив первый аннуитетный платеж в размере 12 000 рублей, мы только 2 000 рублей вернем банку в погашение долга. В следующем месяце кредитования проценты будут начислены по следующей схеме:
998 000 рублей (оставшийся после первого платежа долг) × 1 % (процент за пользование кредита в месяц) = 9980 рублей
Если вычесть из аннуитетного платежа в размере 12 000 рублей сумму процентов в размере 9 980 рублей – при совершении второго аннуитетного платежа в погашение долга уйдет 2020 рублей. По такому принципу можно рассчитать все остальные платежи.
Как Вы видите, сумма аннуитетного платежа остается одна и та же, но доля средств, которые уходят в погашение долга, медленно, но постепенно увеличивается, а сумма процентов медленно, но верно уменьшается. Если представить этот процесс графически, то мы получим вот такую картину:

Формула аннуитетного платежа
Естественно, ни одна кредитная организация не будет рассчитывать аннуитетные платежи по кредиту «на пальцах» и воспользуется одной из многочисленных формул для расчета аннуитетного платежа. Вот одна из них:
АП = Ск × К
где АП – размер аннуитетного платежа, Ск – сумма кредита, К – коэффициент аннуитета.
При этом коэффициент аннуитета рассчитывается следующим образом:
К = ПС/(1– (1+ПС)–м)
где ПС – месячная процентная ставка, равная 1/12 от годовой процентной ставки, М – количество месяцев кредитования.
Условия примера остаются те же. Напомним их: кредит на сумму 1 000 000,00 руб. под 12 % годовых на срок 200 месяцев, уплата процентов и погашение долга производится каждый месяц.
Попробуем рассчитать сумму аннуитетного платежа. Сначала вычислим коэффициент аннуитета: К = 0,01/(1– (1+0,01)–200)=0,01/(1–0,136686381)=0,011583276
А теперь умножим коэффициент аннуитета на сумму кредита: 0,011583276 × 1 000 000 руб. = 11 583,28 руб.
Сумма нашего аннуитетного платежа равна 11 583,28 руб.
Формула аннуитетного платежа в Microsoft EXСEL
Если Вам не хочется рассчитывать аннуитетный платеж вручную, можно воспользоваться специальной формулойаннуитетного платежа в Microsoft Exel, выглядит она так: =ПЛТ(ПС;М;СК)
где ПС – месячная процентная ставка, указанная в виде дроби, в числителе – годовая процентная ставка, в знаменателе – 12 (количество месяцев в году), М – количество месяцев кредитования;
СК – сумма кредита.
Получим ту же сумму, которую мы вычислили вручную, 11 583,28 руб.
И наконец, еще более простой вариант: скачайте вот этот файл, подставьте свои цифры и получите сумму аннуитетного платежа.
источник: http://kredityvopros.ru/banksabout.ru/raschet-annuitetnogo-platezha/
Расчет аннуитетных платежей по кредиту в Excel
Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.
Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1).
Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:
- «Ставка» – годовая процентная ставка по кредиту делённая на 12.
- «Кпер» – общий срок кредитования.
- «Пс» – сумма кредита (указывается со знаком минус).
Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными.
Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4).
После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.
Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ».
По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.
Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.
Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.
В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.
Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:
Расчет в Excel суммы кредита для заданного аннуитетного платежа
В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей.
По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.
Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!

Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами.
Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.
Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:
- «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
- «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
- «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).
Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.
Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4). Те самые параметры, которые мы вводили в таблице функции ПС.
Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:
Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).
Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования.
Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:
Кредитный калькулятор в Excel по расчету графика платежей
Два предыдущих кредитных калькулятора очень удобны, но они выполняют краткие (общие) расчёты. А иногда заёмщику нужна расширенная информация – график ежемесячных аннуитетных платежей с детальной расшифровкой каждой выплаты (с указанием сумм, идущих на погашение процентов, и сумм, погашающих тело кредита).
В общем, сейчас мы сделаем в программе Excel ещё один кредитный калькулятор, который будет автоматически рассчитывать график аннуитетных платежей. Щёлкаем мышкой по рисунку:

Перед вами расширенная и доработанная версия нашего первого кредитного калькулятора (того, который рассчитывает размер ежемесячного аннуитетного платежа по кредиту). Здесь кроме стандартных блоков с исходными данными и расчётами, появилась таблица, в которой детально расписаны все наши будущие ежемесячные выплаты. Таблица имеет пять колонок:
Ежемесячный платёж. Это тот самый аннуитетный платёж, который не меняется на протяжении всего срока кредитования. В сноске к одной из ячеек вы можете увидеть данные, которые внесены в строку формул: =ПЛТ(B3/12;B4;-H14).
Вы уже знаете, что за расчёт аннуитетного платежа в экселе отвечает функция ПЛТ. Координаты необходимых значений для расчёта можно внести, как через строку формул, так и заполнив таблицу, которая появится при нажатии на кнопку «fx», находящуюся слева от строки формул.
Погашение процентов. Здесь рассчитывается доля процентов в аннуитетных платежах (в каждой новой выплате она будет уменьшаться). В программе Excel за расчёт данного показателя отвечает функция ПРПЛТ.
Опять же, задать необходимые параметры для расчётов можно либо нажав на кнопку «fx» и заполнив таблицу, либо просто внеся нужную информацию в строку формул. В нашем примере для расчёта доли процентов в первом платеже, в строке формул записано следующее: =ПРПЛТ(A15/12;D15;B15;-C15).
Погашение тела кредита. Та самая выплата, которая вытягивает нас из долговой ямы и избавляет от банковского рабства. Мы рассчитали её просто: из суммы аннуитетного платежа вычли долю процентов, которую рассчитали в предыдущей колонке. Собственно, в строке формул по первому платежу так и записано: =E15-F15.
Но можно пойти и другим, более изощрённым, путём. В программе Excel за расчёт этого платежа отвечает функция ОСПЛТ. Можете для интереса нажать кнопку «fx», выбрать функцию ОСПЛТ, внести все необходимые данные и получить сумму, идущую на погашение тела кредита в выбранном платеже.
Долг на конец месяца. Ну, здесь всё просто! В данной колонке отображается сумма вашего долга перед банком на конец текущего месяца. Из текущего остатка мы отнимаем долю, идущую на погашение тела кредита. А вот уплаченные проценты просто уходят в казну банка и никак не влияют на сумму вашего текущего долга по кредиту.
источник: www.temabiz.com/finterminy/ap-raschet-annuitetnyh-platezhej-po-kreditu-v-excel.html
Кому выгоден аннуитет?
В первую очередь аннуитетный способ погашения выгоден банку. Объясняется это тем, что в течение всего срока погашения кредита проценты начисляются на первоначальную сумму кредита.
Иными словами, среди двух кредитов с одинаковыми процентными ставками, сроком погашения и дополнительными комиссиями, кредит с аннуитетной схемой погашения всегда будет дороже.
Для примера, рассчитаем переплату по кредиту, рассмотренному выше, но теперь с дифференцированным графиком погашения. Она составит 19 600 000 рублей. Это на 5 693 422 рубля меньше, чем при аннуитетной схеме.
С другой стороны, погашение задолженности и процентов равными долями удобно кредитополучателю, так как ежемесячный платёж является постоянным и не требует уточнения в банке необходимой суммы взноса, в то время как при дифференцированном графике каждый месяц сумма платежа окажется разной.
Применение аннуитетного способа погашения, таким образом, обойдётся дороже, но при этом гораздо удобнее.
источник: https://myfin.by/wiki/term/annuitetnyj-platyozh